Performance comparision of A* vs DLS a Casestudy

Absract

Search algorithms are an essential component of many artificial intelligence applications.Depth Limited Search and A* Search are two popular search algorithms that have been widely used in various domains, including robotics, game playing, and natural language processing. The research paper presents an overview of these two algorithms, their advantages, disadvantages, and areas of application. A detailed comparison of these two algorithms in terms of their performance, efficiency, and effectiveness in solving various search problems is also provided. Finally, the paper presents Python code examples for both algorithms. After performing several runs for each algorithm and graph data, it was found that while the A-star search was able to find the cheaper cost almost always, Depth Limited search was able to find the route faster with fewer node visits.

Introduction to Search Algorithms

The objective of search algorithms is to find a solution to a given problem by exploring a search space of possible solutions. The search space can be represented as a tree or a graph, where each node represents a possible state or configuration of the problem, and the edges represent the possible transitions between states.

Introduction to AI Search Algorithms

Artificial intelligence (AI) search algorithms refer to a group of methods AI systems use to scour a problem space and identify an ideal or nearly ideal response to a specific issue. These methods are employed to search through graphs, forests, or other types of structures for a route or a group of answers that meet a set of requirements.

Depth-First Search (DFS)

DFS is an algorithm that can be used to navigate a tree or graph and is frequently used in artificial intelligence to investigate all potential answers to an issue. It is often combined with other search methods to build more complex AI systems.

Breadth-First Search (BFS)

BFS examines every potential answer at one depth level before moving on to the next. It is useful for finding the shortest route between two locations in a graph or tree.

A* Search Algorithm

A* Search blends DFS and BFS methodologies, employing a heuristic function to direct the search towards the most likely avenue. It is one of the most successful and popular search methods in AI.

Simulated Annealing

Simulated annealing uses probabilistic methods to explore the search universe and find an answer close to the ideal one. It is beneficial for issues where locating the precise optimal answer is challenging.

Genetic Algorithms

Genetic algorithms mimic natural selection to handle optimization issues. They use a community of potential solutions and mutation and selection operators to gradually develop the best solution.

Hill Climbing

Hill climbing is a straightforward optimization method that iteratively improves the answer by moving to a neighboring spot with a better solution. It starts at a random location in the search area.

Uninformed search

Uninformed search is also called blind search. This term means that the search is not given any additional information about the state beyond what is provided in the problem definition. They can only generate successors and distinguish between goal states and non-goal states. All search strategies differ in the order in which nodes are expanded. Strategies for knowing whether one non-target state is more likely than another are called informed or heuristic search strategies. [1]

Figure 1(a) Uninformed Search Techniques

Informed search

It is easy to see that uninformed searches pursue options that lead away from goals just as easily as they pursue options that lead to them. This finds all but the smallest problems that take up an unacceptably large amount of time or space. Informed search attempts to reduce the search work you need to perform by making intelligent decisions about which nodes are selected for traversal. This means that there exists a way to evaluate the probability that a given node is on the solution path. Usually this is done using a heuristic function. [2]

Figure 1(b) Informed Search Techniques

Insight on Depth Limited Search (DLS) and A* Search Algorithms

Two popular search algorithms used in artificial intelligence are depth limited search and A* search. search method with a depth restriction that restricts the search tree's maximum depth.The method investigates every level of the tree starting at the root node and continues until the maximum depth is reached. The method goes back to the previous level and explores the previous branch if a solution is not discovered at that depth. Once the search space has been thoroughly searched or a solution has been located, this process is repeated.

On the other hand, A* search is a heuristic search method that directs the search towards the most promising nodes in the search space using an evaluation function. The algorithm keeps track of a priority queue of nodes that need to be enlarged, where the priority is determined by the sum of the costs associated with getting to each node and the predicted costs associated with getting to the destination node.

Depth Limited Search

Depth Limited Search is a variant of Depth First Search (DFS) where the search is limited to a specified depth. The purpose of the depth limit is to prevent DFS from searching indefinitely, in case the search space has an infinite depth or is too large to be explored entirely. DLS begins at the base node and recursively examines every node at its current level before heading to the next level. If the goal state is not found at the current depth level, the algorithm moves to the next level until the depth limit is reached or the goal state is found [3].

Depth Limited Search Algorithm Steps

1.Determine the start node and search depth

2.Check if the current node is the goal node

a. If not: do nothing

b. If yes: return

c. If the current node is the goal state, return the node.

3. Verify that the present one fits within the limits of the search level.

a. If so, then expand the node and stack all of its descendants.

b. If not: Take no action.

4. Recursively call DLS for each node in the stack, then return to step 2 [1].

Performance assessment

1.Completeness: It is finished if the shallowest goal was successfully attained.

2.Optimality: Non-optimal since the depth could be higher than the node of choice.

Advantages and Disadvantages of DLS

The advantage of DLS is that it saves memory by only examining nodes up to a certain depth limit. This is useful when the search space is too large to be fully explored. However, DLS may not be able to find a solution even if it exists beyond the depth limit. Furthermore, the effectiveness of DLS depends on the choice of depth limit, which can be difficult to determine in advance [4].

Depth Limited Search Applications

Depth-limited search (DLS) is a search algorithm that limits the depth of exploration in a search tree. DLS has some applications in different fields, including:

Artificial Intelligence: DLS can be used in artificial intelligence for search problems where the search space is large, and an exhaustive search is not possible. The algorithm can be used to limit the depth of exploration in a search tree, reducing the search space and improving the search time.

Game Playing: DLS can be used in game playing to limit the search depth when evaluating game states. In games such as chess or checkers, it is not possible to search the entire game tree, and therefore, depth-limited search can be used to limit the depth of exploration and improve the search time.

Natural Language Processing: DLS can be used in natural language processing for tasks such as parsing and machine translation. The algorithm can be used to limit the depth of exploration when searching for the best parse tree or translation, reducing the search space and improving the search time.

Web Crawling: DLS can be used in web crawling to limit the depth of exploration when

crawling websites. The algorithm can be used to limit the number of pages crawled, improving the crawling speed and reducing the load on the web server.

Robotics: DLS can be used in robotics for path planning and obstacle avoidance. The algorithm can be used to limit the depth of exploration when searching for the best path, reducing the search space and improving the path planning time [5].

Performance Analysis

In summary, Depth-limited search (DLS) is a useful search algorithm that can be used in

various fields to limit the depth of exploration in a search tree, improving the search time and reducing the search space. Its applications include artificial intelligence, game playing, natural language processing, web crawling, and robotics.

Case Study of DLS

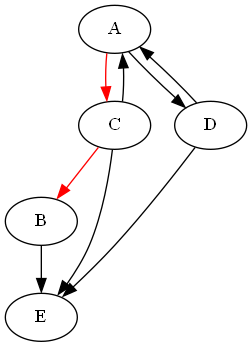
Five nodes (A, B, C, D, and E) make up the graph, and a directed path leads from A to C, then

from C to B.

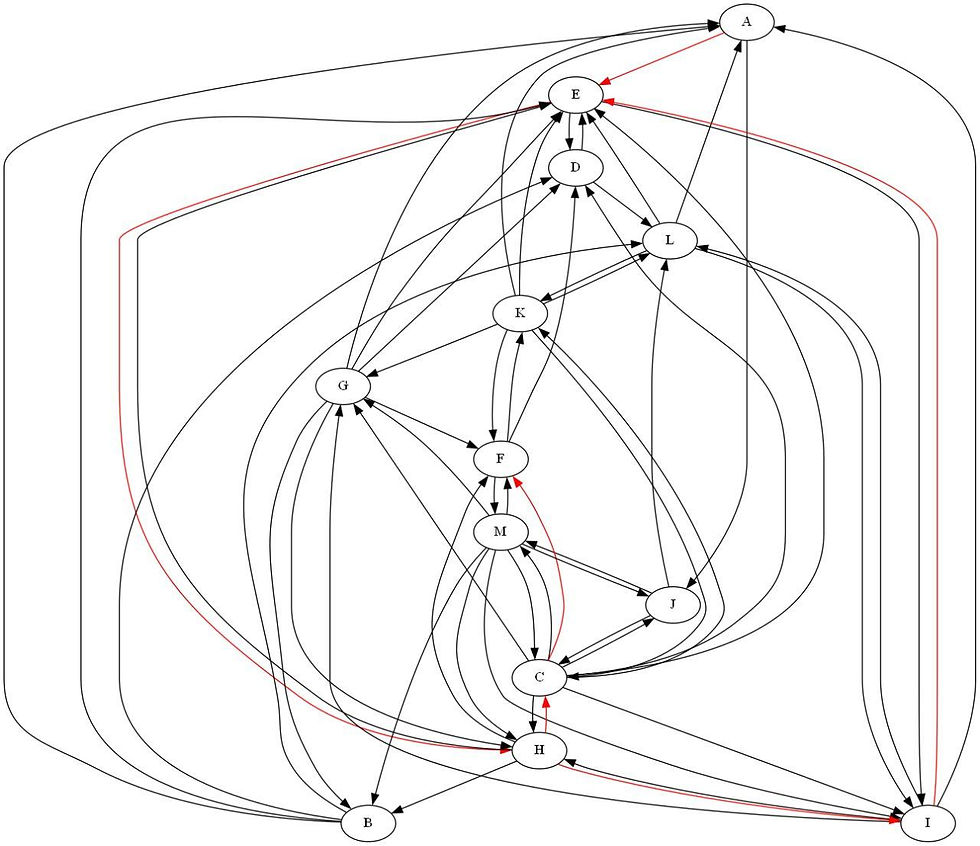
Thirteen nodes (A, B, C, D, E, F, G, H, I, J, K, L and M) make up the graph, and a directed path leads from A to E, then from E to H, then from H to I, then from I to E, then from E to H, then from H to C, then from C to F.

Twenty Six nodes (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y

and Z) make up the graph, and a directed path leads from B to L, then from L to M, then from M to S, then from S to Z, then from Z to T, then from T to D, then from D to Q, then from Q to S, then from S to Z, then from Z to T, then from T to D, then from D to Q, then from Q to S, then from S to K, then from K.

A* Search

A* Search is a well-known search method that directs the search towards the desired state using a heuristic function. The closed list and the open list are both kept up to date by the algorithm. The nodes that have been generated but not yet expanded are found on the open list, while those that have already been expanded are found on the closed list. The algorithm ranks the nodes in the open list according to their f-score, which is calculated by adding their g-score and h-score. The projected cost of traveling from the current node to the destination node is represented by the h-score, while the cost of traveling from the current node to the start node is represented by the g-score [6].

A* Algorithm Steps

This Pseudocode illustrates the steps of A* Algorithm

1. Define a list OPEN. Initially, OPEN consists solely of a single node, the start node x.

2. If the list is empty, return failure and exit.

3. Remove node n with the smallest value of f(n) from OPEN and move it to list CLOSED. If node n is a goal state, return success and exit.

4. Expand node n.

5. If any successor to n is the goal node, return success and the solution by tracing the path from the goal node to x. Otherwise, go to the next step.

6. For each successor node, apply the evaluation function f to the node. If the node has been in either list, add it to OPEN.

7. Repeat from step 2 until an exit condition has been satisfied and the program is terminated [7].

Applications of A* search

A* search is a widely used search algorithm that is used in various domains, including robotics,game playing, natural language processing, and transportation. Here are some of the applications of A* search:

Robotics: A* search is used in robotics for path planning and obstacle avoidance. The algorithm serves in identifying the straightest line that avoids all obstructions between two places.Robotic mapping also uses A* search to determine the best course for navigating uncharted territory.

Game Playing: A* search is used in game playing to find the best move for an agent in a game.The algorithm is used to evaluate different game states and select the move that maximizes the expected outcome. A* search is commonly used in games such as chess, checkers, and other board games.

Natural Language Processing: A* search is used in natural language processing to perform tasks such as parsing and machine translation. The algorithm is used to find the most likely parse tree or translation by evaluating different possibilities and selecting the one with the highest probability.

Transportation: A* search is used in transportation systems to optimize the routing of vehicles.The method is used to determine the fastest route between two sites while taking into account the amount of traffic, roadway closures, and any additional variables that may prolong the journey.

Medical Diagnosis: A* search is used in medical diagnosis to find the most likely diagnosis for a patient based on their symptoms and medical history. The algorithm is used to evaluate different possible diagnoses and select the one that best matches the patient's symptoms and medical history.

Web Search: A* search is used in web search engines to rank web pages based on their relevance to a search query. The algorithm is used to evaluate the relevance of different web pages and rank them based on their relevance score.

In summary, A* search is a versatile search algorithm that is widely used in various domains to solve complex search problems. Its ability to find the optimal path while considering multiple factors makes it an effective tool for solving real-world problems [8].

Case Study for A* search

Five nodes (A, B, C, D, and E) make up the graph, and a directed path leads from A to C, then from C to B.

Thirteen nodes (A, B, C, D, E, F, G, H, I, J, K, L and M) make up the graph, and a directed path leads from A to J, then from J to M, then from M to F.

Twenty-Six nodes (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y

and Z) make up the graph, and a directed path leads from B to D, then from D to J, then from J to K.

Experimental Results and Discussions

Number of nodes: The process of exploring a search space, which is a collection of states or nodes connected by transitions or edges, may be thought of as a search algorithm.

Number of visits: This term describes the quantity of times a certain state or node inside a search algorithm has been traversed during the course of a search. The frequency with which various nodes or states are investigated and assessed throughout search is tracked by this parameter.

Search cost: The term "search cost" often refers to the time or resources needed to run a search algorithm in order to discover a solution to a problem.

Time complexity: The term "time complexity" describes the amount of processing time or

resources needed to solve a given issue in relation to the magnitude of the input.

Space complexity: The concept of "space complexity" refers to the amount of memory or

storage required by an algorithm to solve a problem as an estimate of the dimension of the input.

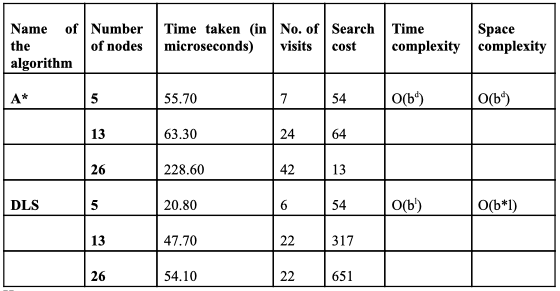
Here,

b = branching factor

l = maximum length path in the search graph

d = depth of solution state from start state

Conclusion and Future Enhancements

A* search and Depth Limited Search (DLS) have been compared in this study, which also looked at their benefits and drawbacks. A* search is an educated search algorithm that directs the search to the destination node using a heuristic function, whereas DLS is an uninformed search method that caps the search depth at a predetermined value. The study paper's trials' findings revealed that A* search outperformed DLS in terms of both time complexity and spatial complexity.

The research topic still has a number of areas that could use improvement. The performance of these search algorithms in more complicated and dynamic contexts is one possible area for development. A* search could also benefit from improvement by investigating the usage of various heuristic functions, as the choice of heuristic function can have a substantial impact on the algorithm's performance.

Additionally, other search algorithms like iterative deepening search, breadth-first search, and depth-first search could be taken into account to further the comparison between A* search and DLS. Additionally, the research could be expanded by examining how well these algorithms perform when applied to various types of issues, including optimization problems, constraint fulfillment problems, and planning challenges.

In conclusion, even though the study paper comparing A* search to DLS highlighted the advantages and disadvantages of these search algorithms, there is still much potential for development and additional research in this field.

References

[1] S. R. a. P. Norvig, “Artificial Intelligence: A Modern Approach, 4th Edition,” Pearson Publication.

[2] D. W. Patterson, “Introduction to Artificial Intelligence & Expert Systems,” Prentice-Hall.

[3] “What is depth limited search? (educative.io)”. [Online]. Available:

https://www.educative.io/answers/what-is-depth-limited-search

[4] “Depth Limited Search (opengenus.org)”. [Online]. Available: https://iq.opengenus.org/depth-

limited-search/

[5] “Uninformed Search Algorithms - Javatpoint”. [Online]. Available:

https://www.javatpoint.com/ai-uninformed-search-algorithms

[6] “What is Heuristic Search - Techniques & Hill Climbing in AI - DataFlair (data-flair.training)”.

[Online]. Available: https://data-flair.training/blogs/heuristic-search-ai/

[7] “A* Search Algorithm (slideshare.net)”. [Online]. Available:

https://www.slideshare.net/vikasdhakane/a-search-algorithm

[8] “Machine Learning: Algorithms, Real-World Applications and Research Directions |

SpringerLink”. [Online]. Available: https://link.springer.com/article/10.1007/s42979-021-

00592-x